应用密码学
0.总体大纲

1. 密码学概念
(1) 密码学的学科特点
- 数学基础:密码学是一门基于数学理论和算法的学科,需要熟练掌握数学知识。
- 多学科交叉:密码学不仅仅是数学学科,还涉及计算机科学、信息安全、电子工程等多个领域,需要跨学科合作。
- 应用广泛:密码学在现代社会中有着广泛的应用,如网络安全、电子商务、金融交易、政府通信等。
- 不断发展:随着计算机技术的不断进步,密码学也在不断发展,需要及时跟进最新的研究成果和技术进展。
- 安全性:密码学的主要目标是确保信息的机密性、完整性和可用性,因此安全性是其最重要的特点之一。
(2)研究的主要内容
密码编码学和密码分析学
机密性、完整性、鉴别、抗抵赖
(3)密码系统的安全条件:理论不可破详和实际不可破译,实际可用密码系统须具备的特性。
略
(4)掌握对密码系统的4种攻击方式的特点
唯密文攻击(被动)这种攻击方式通常是密码分析中最困难的一种,因为攻击者只能通过分析密文的统计特性和密文的结构来猜测明文和密钥。需要攻击者拥有大量的密文和足够的时间和计算资源来破解密码系统
已知明文攻击(被动)攻击者已经知道了一部分的明文和密文,可以通过比对明文和密文之间的关系来推断出密钥。需要攻击者在攻击之前收集到一些明文和密文的对应关系。
选择明文攻击(主动)攻击者可以选择一些明文,获得对应的密文,以此来推断出密钥。可以选择任意的明文,可以更加精准地推断出密钥。需要攻击者能够向密码系统发送恶意的明文。
选择密文攻击(主动)攻击者可以选择一些密文,获得对应的明文或其他密文,以此来推断出密钥。需要攻击者能够向密码系统发送恶意的密文。
(5) 正确理解密码系统安全性原则:“切秘密寓于密钥之中”
(柯克霍夫斯(Kerckhoffs)原则)密码体制的安全性仅应依赖于对密钥的保密,而不应依赖于对算法的保密。只有在假设攻击者对密码算法有充分的研究,并且拥有足够的计算资源的情况下仍然安全的密码才是安全的密码系统。不把密码系统的安全性建立在算法保密性上,意味着密码算法可以公开,也可以被分析,即使攻击者知道密码算法也没有关系。
(6) 两类重要密码体制,即对称密码体制和非对称密码体制的主要特点
对称密码体制(常规密码体制、秘密密钥密码体制)对明文/密文变换时,加解密密钥相同,或可相互导出;
双方在通信前需要安全地协商共享密钥;
加解密算法效率较公开密码算法高;
系统开放性差,密钥管理复杂;
不能提供抗抵赖服务。
非对称密码体制 (公钥密码体制、公开密钥密码体制)对明文/密文变换时,加解密密钥不相同,且不能由加密密钥(公钥,公开) 导出解密密钥 (私钥,保密);
系统开放性好,密钥管理较容易可提供抗抵赖服务(数字签名)
加解密运算复杂,效率低,不宜作数据加密.
存在特有的“可能报文攻击”的威胁。
(7) 两种保密通信模型及原理
- 点对点保密通信模型
是指通信双方之间进行加密通信,以保护通信内容的机密性和完整性。在点对点保密通信模型中,通信双方需要使用相同的密钥来进行加密和解密。
点对点保密通信模型的原理是基于对称加密算法,通信双方需要事先协商好一个密钥,并使用该密钥来进行加密和解密。在通信过程中,明文消息被加密成密文,只有使用正确的密钥才能将密文解密成明文。
点对点保密通信模型的优点是加解密速度快,但需要保证密钥的安全性。
- 多方保密通信模型
是指多个参与者之间进行加密通信,以保护通信内容的机密性和完整性。在多方保密通信模型中,每个参与者需要使用不同的密钥来进行加密和解密。
多方保密通信模型的原理是基于公钥加密算法和数字签名算法。在多方保密通信过程中,每个参与者都有自己的公钥和私钥,公钥用于加密和验证数字签名,私钥用于解密和签名。在通信过程中,每个参与者可以使用其他参与者的公钥来加密消息,只有使用正确的私钥才能解密消息。同时,参与者还可以使用自己的私钥对消息进行签名,以保证消息的真实性和完整性。
多方保密通信模型的优点是可以保证通信内容的机密性、完整性和真实性,但加解密速度较慢,并且需要管理多个密钥。
2.古典密码技术
(1)替代密码与置换密码的概念与表示方法
替代(替换)密码
•替代密码是指先建立一个替换表,加密时将需要加密的明文依次通过查表,替换为相应的字符,明文字符被逐个替换后,生成无任何意义的字符串,即密文,替代密码的密钥就是其替换表 ;
•根据密码算法加解密时使用替换表多少的不同,替代密码又可分为单表替代密码和多表替代密码。
单表替代密码: 密码算法加解密时使用一个固定的替换表;
多表替代密码: 密码算法加解密时使用多个替换表。
置换密码
•置换密码又称为换位密码;
•置换密码通过改变明文消息各元素的相对位置,但明文消息元素本身的取值或内容形式不变;
•在前面的替代密码中,则可以认为是保持明文的符号顺序,但是将它们用其它符号来替代。
置换密码在实质上是Hill密码的特例。所以置换密码属线性变换的密码。
(2)单表替换密码、多表替换密码的概念
单表替换密码:一般单表替代密码、移位密码、仿射密码、密钥短语密码
一般单表替代密码的原理是以26个英文字母集合上的一个置换π为密钥,对明文消息中的每个字母依次进行变换。
·密钥空间K很大,|K|=26!=4×1026 ,破译者穷举搜索计算不可行,1微秒试一个密钥,遍历全部密钥需要1013年。
·移位密码体制是替换密码体制的一个特例,它仅含26个置换做为密钥空间。
·密钥_π_不便记忆。
多表替代密码的特点是使用了两个或两个以上的替代表。
多表替换密码:维吉尼亚密码、Hill密码、一次一密密码、Playfair密码
(3)掌握 Hill 密码的特性与计算方法
Hill密码算法的基本思想是通过线性变换将_n_个明文字母转换为_n_个密文字母。解密只需做一次逆变换即可。
3.机密性
对称密码
分组密码
总体共性
分组密码体制(Block cipher)是在密钥_k_控制下一次变换一个明文数据块的密码体制
具有速度快、易于标准化和便于软硬件实现等特点
在计算机通信和信息系统安全领域有着最广泛的应用
针对安全性的两个基本原则:
·混淆原则(Confusion) :又称混乱原则、扰乱原则等,是指将密文、明文、密钥三者之间的统计关系和代数关系变得尽可能复杂(主要利用复杂的非线性替换算法)
·扩散原则(Diffusion) :将明文的统计规律和结构规律散射到相当长的一段统计中去(最简单的方法是迭代换位(置换))
乘积和迭代机制有助于实现混淆和扩散
分组加密算法的两个基本结构:SPN与Feistel:
SPN结构也是一种特殊的迭代密码 ,SPN结构和Feistel结构相比,可以得到更快速的扩散,但是SPN密码的加解密运算通常不完全相同。** **
Feistel 密码密文的任何一位均与明文和密钥的每一位相关;而明文和密钥的任何一位的变化将影响到尽量多的密文,其中函数 f 用于产生扩散和混淆作用,但并不要求为可逆函数;
DES
数据分组长度、密文分组长度为64位,
使用的密钥为64位,但有效密钥长度为56位(有8位用于奇偶校验)。
16轮迭代的Feistel密码算法。
DES由初始置换,16轮迭代,初始逆置换组成
DES基本运算操作:置换、替换、异或与循环移位
解密算法和加密相同,但子密钥的使用顺序相反。
体制是公开的,系统的安全性完全靠密钥的保密
S盒设计特点:(1) 任何S盒都不是输入变量的线性函数;
(2) S盒的每一行(除输入比特的最左和最右比特确定) 包括所有16种比特组合;
(3) 改变S盒的1个输入位,至少引起2位的输出变化;
(4)当固定S盒的1位输入时,S盒的每一位输出中0和1的个数尽可能平衡
Festial结构特性主要优点:
1.设计容易: f 函数不要求可逆, 加、解密算法结构相同;
2.强度高:如果 f 函数是随机的,则连续若干轮复合形成的函数与随机置换是无法区分的.
主要缺点:
- 每轮加密时输入有一半没有改变;
- 左右块的加密处理不能并行实施
Feistel模型至少需要3轮才可实现完全性, 且当其F函数具有完全性时,只需3轮即可实现完全性,此时DES算法需且只需5轮即可实现完全性
重点:DES算法的互补对称性


AES
明文和密文长度128位,密钥长度可变(128/192/256位)
加解密使用不同的算法
置换、代替、代数运算
SP结构,基本轮函数迭代,迭代轮数可变(≥10)
字节替代 SubByte ()、行移位变换 ShiftRows()、列混合变换 MixColumns()、轮密钥加法 AddRoundKey()
ByteSub( )与ShiftRows( )运算次序可交换
列混合MixColumns()为线性变换
分组密码的操作方式
ECB
将每块明文加密成相应的密码块,若最后一块不足64bit,则用一些任意二进制序列填充
特点 : (1) 一种最简易的工作方式;
(2) 相同密钥作用下,密文块与明文块一一对应,易于暴露明文的固有格式;
(3) 各密文块间缺乏相关性,信息易于受到块替换攻击
CBC
加入反馈机制,当前明文块在加密之前要与前面的密文块进行异或
特点 : (1) 同一明文块会产生不同的密文块;
(2) 有误码扩散,若Ci在传送过程中出错,则解密时会造成mi和mi+1两个明文块都出错,
但后面的密文块仍然能自动正确恢复;
(3) 只有当所有64比特块到达后才能开始编解码
CFB
为克服CBC方式的第(3)个问题,数据是按比分组小得多的单位进行加密的,密文依赖于前面所有的明文
特点 : (1) 移位寄存器的的内容与明文整个以前的历史有关,同样需要一个初始向量(寄存器初值);
(2) 将分组密码转换为流密码(序列密码),实现即时加密;
OFB
与CFB模式相似,但它是在块内部进行反馈,其反馈机制既不依赖明文也不依赖密文流
特点 : (1) 没有误码扩散,适用于传输信息长度变化较大的数据,如语音、图像等。
(2) 比CFB更易受对消息流的篡改,攻击者对密文的篡改难以检测。
(3) 链接相关性,密文与前面的明文无关。
(4) 应用时要求一次一密方式 (OTP,One-Time Pad)
CTR(计数器模式)
特点 : (1)具有随机访问特性,可随机对任意一个密文分组进行解密处理;
(2)处理效率高,可进行并行处理,提高数据吞吐量;
(3)同一明文块会产生不同的密文块;
(4)可提前进行预处理;
(5) 实现简单,加、解密阶段都只涉及加密函数。
3DES
二重DES的加密,所用密钥的长度为 :
56×2=112 bits,二重DES很难抵挡住中间相遇攻击法
到目前为止,还没有人给出攻击三重DES的有效方法,相对于单一DES来说,复杂性以指数形式增长。
IDEA
是对64bit大小的数据块加密的分组加密算法,密钥长度为128位
IDEA与DES的比较:
共同点:同属分组密码体制(分组长度也为64比特)
不同点:(1)IDEA密钥长度128位;
(2) IDEA的加解密子密钥不完全相同(但可相互导出);
(3) IDEA可用软硬件实现,但倾向于软件实现;
(4) DES为Feistel结构,而IDEA不是。
RC5
RC5加密明文块的长度为32,64,128 bits。并且对应同样长度的密文。密钥长度为从8到2040 bits
SM4
·加解密算法及密钥扩展都采用32轮非线性迭代结构。
·数据分组长度、密钥长度=128位(16Byte)
·算法具有对合特性:解密算法和加密算法结构相同,只是轮密钥反序使用(与DES类似)
·密码结构:非对称Feistel结构
序列密码
序列密码又称为流密码(stream cipher),它是一种对称密码体制,
特点:
l 明文消息按字符或比特逐位进行加密;
l 基于硬件电路实现,如链路密码机;
l 实现简单,加解密处理速度快;
l 没有或只有有限的错误传播;
l 多用于军事和外交等特殊通信领域。
密钥流序列具有如下性质:
Ø极大的周期
Ø良好的统计特性
Ø抗线性分析
同步序列密码
系统内部记忆元件的状态独立于明文或密文的叫做同步流密码,否则叫自同步流密码。
分组密码的OFB模式就是一个同步序列加密的例子。
特点:
l 无错误传播
l 有同步要求
自同步序列密码
密钥流的产生与己经产生的一定数量的密文有关。
分组密码的CFB模式就是一个自同步序列加密的例子。
特点:
l 密钥流的产生与密文有关
l 有限错误传播
l 自同步
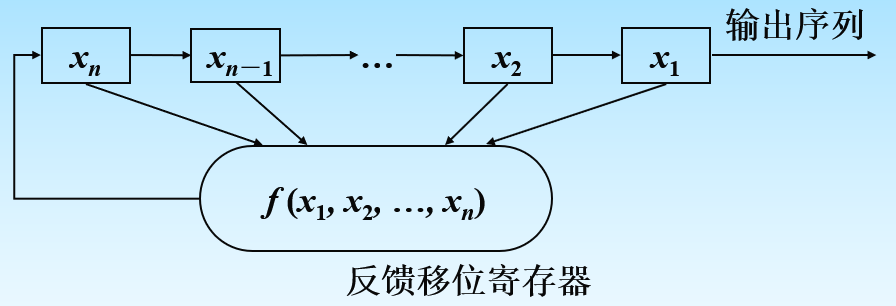
LFSR-线性反馈移位寄存器
定义如果一个GF(2)上的n阶反馈移位寄存器的反馈函数形如
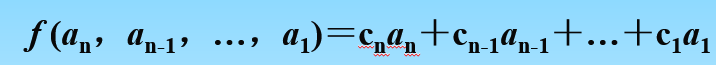
其中ci∈GF(2),1≤i≤n,则称其为线性反馈移位寄存器。否则,称其为非线性反馈移位寄存器。
如果直接用线性移位寄存器序列作为密钥序列,则在已知明文攻击的情况下,相应的序列密码体制是很不安全的。
可以对一个或多个线性移位寄存器序列进行非线性组合来获得在序列密码中安全性良好的非线性序列
基于LFSR的序列密码生成器:
Geffe生成器
钟控生成器
交错停走式生成器
RC4
密钥长度可变的流加密算法簇
其核心部分的S-box长度可为任意,但一般为256字节。
RC4算法的原理较简单,主要有两个算法:
(1)密钥调度算法KSA
(2)伪随机数生成算法PRGA
密钥调度算法的作用是将一个随机密钥(典型大小是40位~256位)变换成一个初始置换,即相当于初始化状态矢量S,然后伪随机数生成算法PRGA利用该初始置换生成一个伪随机输出序列。
加密时,将K的值与下一个明文字节异或;
解密时,将K的值与下一个密文字节异或。
为了保证安全强度,目前的RC4至少使用128位的密钥。
非对称密码
概述
公钥密码又称为双钥密码和非对称密码,是1976年由Diffie和Hellman提出
对公钥密码的要求 :
(1) 生成密钥对的计算很容易;
(2) 发送方A用接收方B的公钥PKB生成密文c,计算上是容易的。 c = EPKB(m)
(3)接收方B用自己的私钥SKB对 c 解密,在计算上是容易的。 m = DSKB (c) = DSKB(EPKB(m))
(4)攻击者通过B的公钥PKB计算出私钥SKB在计算上不可行。
(5)攻击者通过B的公钥PKB和密文c还原明文m在计算上不可行。
三类算法: RSA, ElGamal, ECC
(1) RSA
–基础: IFP(Integer Factorization Problem)
–加/解密、密钥交换、数字签名
–使用最广泛
(2)ElGamal
–基础: DLP(Discrete Logarithm Problem)
–加/解密、密钥交换、数字签名
(3)ECC
–基础: ECDLP(Elliptic Curve Discrete Logarithm Problem)
–加/解密、密钥交换、数字签名
–密钥短,速度快
** –已开始广泛应用**
RSA
RSA的基本性质 :
(1)加密和解密运算具有可交换性
(2)加解密算法的有效性
(3)在计算上由公开的加密密钥不能求出解密密钥
RSA的算法描述 :

ElGamma
密文空间大于明文空间。明文空间为Zp,而密文空间为 Zp× Zp,也即对于每个明文,其密文由2个Zp上的元素组成
ElGamal加密体制通过明文 m乘以yBk掩盖明文,产生c2 ;同时值c1 = ak也作为密文的一部分进行传送。
ElGamal公开密钥密码算法的安全性建立在计算Zp上离散对数的困难性上
要使用不同的随机数k来加密不同的信息
随机数k不可预测

ECC-椭圆曲线密码体制
“椭圆曲线”并非一定是椭圆,是指由二元三次方程: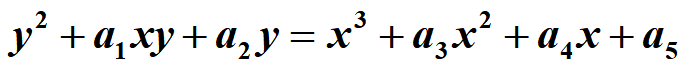
所描述的曲线
M-V
M-V 公钥密码体制即是在椭圆曲线上的一个有效实现

SM2
SM2是一种基于椭圆曲线密码学的公钥密码算法,由中国密码标准化工作组推荐
SM2算法的主要内容包括3部分:
数字签名算法;密钥交换协议;公钥加密算法;
SM2算法的特点如下:
- 安全性高:SM2算法采用了椭圆曲线密码学中的离散对数问题,能够提供较高的安全性。
- 签名速度快:SM2算法的签名速度比传统RSA算法要快,适合用于大量数据的签名操作。
- 密钥长度短:SM2算法的密钥长度比传统RSA算法要短,节省了存储空间和传输带宽。
- 支持国密标准:SM2算法是中国国家密码局发布的国家密码算法标准,符合国密要求,
- 公开透明:SM2算法设计和安全性分析是公开透明的,有助于对算法的安全性进行评估和验证。
4.完整性
鉴别是通过验证用户或实体的身份以确保其合法性的过程可以将鉴别分为两种类型:报文鉴别和实体鉴别。
- 报文鉴别:报文鉴别是指通过加密算法或哈希算法对报文进行处理,生成报文的认证码或数字签名,并将其附加在报文中,以确保报文的完整性和真实性。
- 实体鉴别:实体鉴别是指验证通信实体的身份,以确保通信双方的身份认证和数据传输安全。
报文鉴别
基于加密
略
基于hash
(1)密码散列函数的概念和6个基本性质
密码学中的散列函数又称为哈希函数(Hash函数)杂凑函数,它是一种单向密码体制,是一个从明文到密文的不可逆映射,只有加密过程,没有解密过程。
设散列函数为h(m),其有以下基本特性:
(1)h(m)算法公开,不需要密钥。
(2)具有数据压缩功能,可将任意长度的输入数据转换成一个周定长度的输出。
(3)对任何给定的 m,h(m)易于计算
(4)具有单向性。给定消息的散列值h(m),要得到消息m在计算上不可行;
(5)具有弱抗碰撞性(Weak Collision Resistance,也称弱抗冲突性)。对任何给定的消息m,寻找与m 不同的消息m使得它们的散列值相同即h(m)=h(m),在计算上不可行。
(6)具有强抗碰撞性(Strong Collision Resistance,也称强抗冲突性)寻找任意两个不同的消息m和m使得h(m)-h(m)在计算上不可行。
(2) 理解哈希函数的抗碰撞安全性
所谓散列函数的碰撞是指若两个消息m与m’,m不等于m’,但它们的散列值相等,即h(m)=h(m’),那么,则把这种情况称为发生了碰撞或冲突。由于输入消息的长度可以是任意的,但散列函数输出的散列值的长度是固定的,如对于散列值长度为160位的散列函数而言,可能的散列值总数为 2^160。显然,不同的消息就有可能会产生相同的散列值,即散列函数具有碰撞的不可避免性。但是,散列算法的安全性要求找到一个碰撞在计算上是不可行的。也就是说,要求碰撞是不可预测的,攻击者不能指望对输入消息的预期改变可以得到一个相同的散列值。
** (3)散列函数的基本应用方式(基于散列函数的 6 种报文鉴别方式,掌握 P93,图 5.16)**
利用密码技术设计提供信息的机密性、完整性和可鉴别性服务的信息安全传输方案
** (4) 单向散列函数的设计、构造问题**
简单的散列函数的不安全性
- 易于碰撞攻击:简单的散列函数通常使用较短的散列值,因此很容易出现碰撞,即不同的输入数据产生相同的散列值。攻击者可以利用碰撞来欺骗系统,从而执行未经授权的操作。
- 易于彩虹表攻击:攻击者可以构建彩虹表,其中包含了所有可能的输入数据及其对应的散列值。然后,攻击者可以将目标散列值与彩虹表中的散列值进行比较,以找到对应的输入数据。
- 易于字典攻击:攻击者可以使用已知的密码字典或常见密码列表来生成散列值,并将其与目标散列值进行比较。由于简单的散列函数通常使用较弱的算法,因此很容易受到字典攻击的影响。
- 易于生日攻击:如果散列函数的输出长度较短,攻击者可以使用生日攻击来寻找碰撞。生日攻击利用概率学原理,在较短的时间内就能找到相同的散列值。
散列函数的生日攻击问题
与散列函数相关的类似问题可表述如下:给定一个散列函数h的输出长度为m位,共有2^m个可能的散列值输出,如果让散列函数h接收k个随机输入产生集合X,再使用另外k个随机输入产生集合Y,问必须为多大才能使两个集合产生相同散列值输出的概率大于0.521
这时,n=2^m,由式(5.3)有: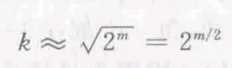
这种寻找散列函数h的具有相同输出的两个任意输入的攻击方式称为生日攻击。
下面举一个简单的示例来说明这种针对散列函数的生日攻击过程。还是假设 Alice是一家计算机公司的总经理,要从Bob的公司购买一批计算机。经过双方协商,确定了5000 元/台的价格,于是 Bob 发来合同的电子文本征得 Alice 的同意,Alice确认后计算出这一合同文本的散列值,用自己的私钥进行数字签名并发回给 Bob,以此作为 Alice对合同样本的确认。
但是,Bob在发给Alice 合同样本前,首先写好一份正确的合同,然后标出这份合同中无关紧要的地方。由于合同总是由许许多多的句子构成的,而这些句子往往可以有很多不同的表达方式,所以一份合同总可以有很多种不同的说法,却都能表达同样的意思。现在Bob只要把这些意思相同的合同都列出来作为一组,然后再把每一份合同当中标明的价格从5000元/台改为10000元/台,并且把修改过的合同也集中起来作为另外一组,这样他的手中就有了两组合同:一组的价格条款都是 5000元/台的,而另一组的价格都是 10000元/台然后,Bob只要把这两组合同的散列值都计算一遍,从当中挑出一对散列值相同的,把这一对当中的那份写明5000元/台的合同作为合同样本给Alice,并交由Alice进行签名而自己则偷偷把那份10000元/台的合同藏起来,以便在将来进行欺诈。
从生日攻击的理论上来讲,如果假设上述事例使用的散列函数输出为64位,那么 Bob只要找到合同中32个无关紧要的地方,来分别构成5000元/台和10000元/台两组合同,有0.5以上的概率能在这两组合同中找到碰撞,来实现他的诈骗行为。
MD5
略
SHA-1
输入:最大长度为264-1位的消息;
输出:160位消息摘要;
处理:输入以512位数据块为单位处理
SHA-256

SM3
SM3密码杂凑算法的设计主要遵循以下原则:
- 能够有效抵抗比特追踪法及其他分析方法;
- 软硬件实现需求合理;
- 在保障安全性的前提下,综合性能指标与SHA-256同等条件下相当
数字签名(实体鉴别)
(1) 数字签名的概念,基本特性
数字签名实际上是一个把数字形式的消息和某个源发实体相联系的数据串,把它附加在一个消息或完全加密的消息上,以便于消息的接收方能够鉴别消息的内容,并证明消息只能源发于所声称的发送方。
迅速的、远距离的、更高的安全性
(1)签名是不可伪造的。
(2)签名是不可抵赖的。
(3)签名是可信的。
(4)签名是不可复制的。
(5)签名的消息是不可篡改的。
(2) 数字签名两种执行方式
1.直接方式
直接方式是指数字签名的执行过程只有通信双方参与,并假定双方有共享的秘密密钥,或者接收一方知道发送方的公开密钥。例如消息接收者可以获得消息发送者的公钥,发送者用其自己的私钥对整个消息或者消息散列码进行签名来形成数字签名。直接数字签名有一些共同的缺点:方案的有效性依赖于发送方秘密密钥的安全性。如果发送方想对已发出的消息予以否认,就可以声称自己的秘密密钥已丢失或者被盗,因此自己的数字签名是他人伪造的。可以采取某些行政管理手段,虽然不能避免,但可在某种程度上减弱这种威胁。例如,要求每一个被签名的消息都包含一个时间戳,标明消息被签名的日期和时间,并要求秘密密钥一旦丢失,就要立即向管理机构报告。但这种方式的数字签名仍然存在着假冒签名的威胁,假设发送方的秘密密钥在时间T被窃取,攻击者可以伪造一个消息,用发送方的秘密密钥对其签名并加上丁以前的时间戳。
2.具有仲裁的方式
具有仲裁的数字签名是在通信双方的基础上引人了第三方仲裁者参与。通常的做法是所有从发送方到接收方的签名消息首先送到仲裁者,仲裁者将消息及其数字签名进行一系列的测试,以检查其来源和内容,并将消息加上时间戳,与已被仲裁者验证通过的数字签名一起发送给接收方。在这种方式下,仲裁者扮演裁判的角色,起着重要作用并应取得所有的参与者的信任。下面给出几个需要仲裁者的数字签名方案。其中S表示发送方,R表示接收方,A是仲裁者,m是传送的消息。
方案一:对称加密,仲裁者可以看到消息内容
方案二:对称加密,仲裁者不能看到消息内容
方案三:公钥加密,仲裁者不能看到消息内容
(3)数字签名的应用过程
(1)系统的初始化过程:产生的数字签名方案中用到的一切参数,有公开的,也有秘密的。
(2)签名产生过程:此过程用户利用给定的算法对消息产生签名,这种签名过程可公开也可不公开。
(3)签名验证过程:验证者利用公开验证方法对给定消息的签名进行验证,得出签名的有效性。
(4) 热练掌握典型公明密码体制的数字签名算法(RSA、EIGamal、ECDSA)原理、计方法与应用
ElGamal:

(5) 了解国密SM2
SM2是一种基于椭圆曲线密码学的公钥密码算法,由中国密码标准化工作组推荐
SM2算法的主要内容包括3部分:
数字签名算法;密钥交换协议;公钥加密算法;
SM2算法的特点如下:
- 安全性高:SM2算法采用了椭圆曲线密码学中的离散对数问题,能够提供较高的安全性。
- 签名速度快:SM2算法的签名速度比传统RSA算法要快,适合用于大量数据的签名操作。
- 密钥长度短:SM2算法的密钥长度比传统RSA算法要短,节省了存储空间和传输带宽。
- 支持国密标准:SM2算法是中国国家密码局发布的国家密码算法标准,符合国密要求,
- 公开透明:SM2算法设计和安全性分析是公开透明的,有助于对算法的安全性进行评估和验证。
5.身份鉴别技术
(1) 身份鉴别的基本方式(鉴别实体所知、所拥有、所具有的唯一特征)
验证实体所知什么,如一个秘密的口令或通行字。
验证实体拥有什么,如信物、通行证、智能IC卡。
验证实体不可改变的特性,如指纹、声音等生物学测定得来的标识特征。
(2)基于动态口令的身份鉴别原理与实现方案
一次性口令的主要思路是:在登录过程中加入不确定因素,使每次登录传送的鉴别信息都不相同,以提高登录过程安全性。
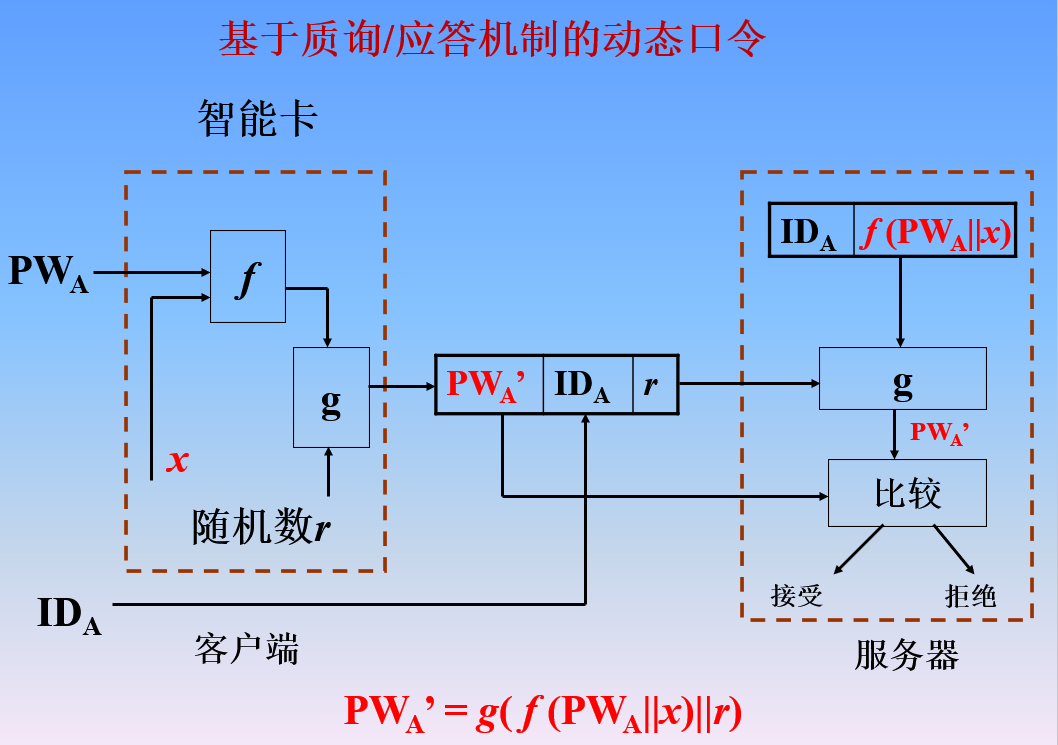
(3)密码协议对抗重放攻击的两种基本方法(时间戳、质询-响应机制)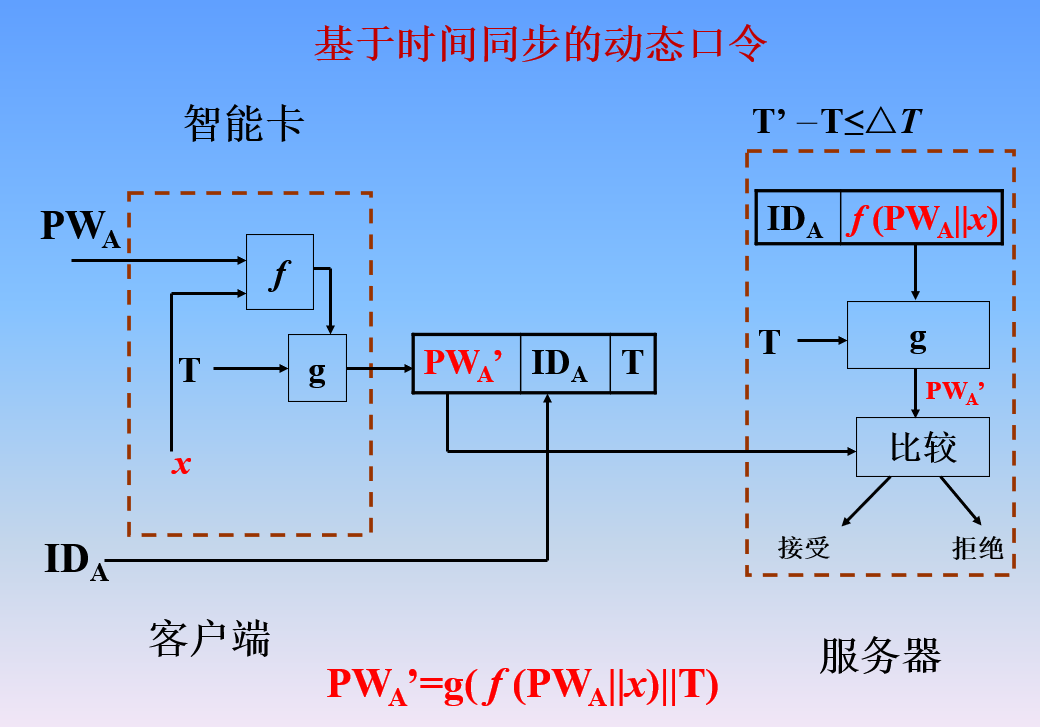
(4) Kerberos 系统的密码学特点(基于对称密码体制)和基本原理
Kerberos 是一种网络身份验证协议,它基于对称密码体制来提供身份验证和授权服务。Kerberos 的密码学特点主要包括以下几个方面:
- 对称加密算法:Kerberos 使用对称密码体制中的加密算法来保证通信机密性,这些算法包括 DES、3DES、AES 等。
- 密钥分发:Kerberos 采用密钥分发技术,即在用户登录时,Kerberos 服务器会向用户分发一个临时密钥(也称为票据授权票据TGT),用户在后续的通信中使用该密钥来进行身份验证和授权。
- 时钟同步:Kerberos 要求网络中所有的计算机时钟都要与 Kerberos 服务器的时钟同步,以避免时钟漂移带来的安全问题。
Kerberos 的基本原理如下:
- 身份验证:用户在本地计算机上输入用户名和密码,本地计算机将该信息发送给 Kerberos 服务器。Kerberos 服务器验证用户信息的正确性,如果验证通过,Kerberos 服务器向用户发送一个 TGT,该 TGT 包含了用户的身份信息和一个临时密钥。
- 授权:用户在访问网络资源时,需要提供 TGT,并向 Kerberos 服务器发起请求。Kerberos 服务器验证 TGT 的正确性,如果通过,就向用户发送一个服务票据(Service Ticket),该票据包含了用户的身份信息和一个用于访问特定资源的临时密钥。
- 资源访问:用户使用服务票据来访问网络资源,本地计算机将服务票据发送给资源服务器进行验证,如果通过,用户得到了访问资源的权限。
总之,Kerberos 是一种安全可靠的身份验证协议,它基于对称密码体制,通过密钥分发、时钟同步等技术来确保安全性和可靠性。
6.抗抵赖
对称、非对称加密,数字签名
7.密钥管理
(1)管理基本内容和概念
密钥管理是一门综合性的技术,涉及密钥的产生、检验、分发、传递、保管、使用、销毁的全部过程,还与密钥的行政管理制度以及人员的素质密切相关。
决定整个密码体制安全性的因素是密钥的保密性(“一切秘密予于密钥之中!”)
(2)理解密钥分配与密钥协商的目标与特点
密钥分配与密钥协商过程都是用以在保密通信双方之间安全建立通信所使用的密钥的协议(或机制)
密钥分配
保密通信中的一方(包括可信第三方)生成并选择秘密密钥,然后将其安全地传送给通信的相关各方。典型协议:Kerboros密钥分配协议
密钥协商
通常是一种协议,利用该协议通信双方可以在一个公开的信道上通过相互传送一些消息来共同建立一个安全的共享秘密密钥。在密钥协商中,双方共同建立的秘密密钥通常是双方输入消息的一个函数。典型协议: Diffie-Hellman密钥交换协议
(3)掌握公钥证书的概念与基本内容,以及证书真实性、有效性的确认(包括用 CA 的公验证数字签名),持有人的确认方法。
公钥证书是一种数字证书,用于验证公钥的真实性和所有者的身份。它包含公钥、所有者的身份信息和证书颁发机构(CA)的数字签名。以下是公钥证书的基本内容:
- :证书中包含了CA的数字签名,以证明该证书是由CA签署的。
为了确认证书的真实性和有效性,需要使用CA的公钥验证数字签名。这个过程包括以下步骤:
- 获取CA的公钥:从CA的网站或其他可靠来源获取CA的公钥。
- 验证数字签名:使用CA的公钥验证证书中的数字签名。如果数字签名可以被验证,则证明证书是由CA签署的,因此证书是真实和有效的。
对于证书的持有人来说,他们可以通过以下方法确认其证书的真实性和有效性:
- 查看证书信息:检查证书中包含的信息是否与自己的身份信息匹配。如果信息不匹配,则证书可能是伪造的。
- 验证数字签名:使用CA的公钥验证证书中的数字签名。如果数字签名可以被验证,则证明证书是由CA签署的,因此证书是真实和有效的。
- 核实证书颁发机构:查看证书中的颁发机构,并确保该机构是可信任的CA。
- 检查证书有效期:确保证书在有效期内。如果证书已过期,则证书不再有效。
(4)Diffie-Hellman 密钥交换算法及安全性基础,熟练掌握计算方法及应用中的相关问题。
Diffie-Hellman(DH)密钥交换算法是一种基于离散对数问题的公钥密码学算法,用于在不安全的通信信道上安全地交换密钥。DH 算法的安全性基于离散对数难题,即给定一个大素数 p,以及 a 和 b 两个整数,计算 a^x mod p 和 b^y mod p 的值很容易,但是由 a^x mod p 和 b^y mod p 计算出共享密钥 g^(xy) mod p 则非常困难。
DH 密钥交换算法的基本原理如下:
- 双方协商素数:双方预先协商一个大素数 p 和一个原根 g。
- 双方生成私钥:双方分别生成自己的私钥 x 和 y,私钥是一个随机数。
- 双方计算公钥:双方分别根据自己的私钥和协商的素数和原根计算出自己的公钥。
- 双方交换公钥:双方将自己的公钥传输给对方。
- 双方计算共享密钥:双方使用对方传输过来的公钥以及自己的私钥计算出共享密钥。
DH 密钥交换算法的计算方法如下:
- 双方协商素数:选取一个大素数 p 和一个原根 g。
- 双方生成私钥:生成一个随机数 x 和 y,作为自己的私钥。
- 双方计算公钥:计算出公钥 A 和 B,其中 A = g^x mod p,B = g^y mod p。
- 双方交换公钥:将 A 和 B 传输给对方。
- 双方计算共享密钥:计算出共享密钥 K,其中 K = B^x mod p = A^y mod p。
DH 密钥交换算法的安全性主要基于离散对数难题,即计算出共享密钥 K 非常困难。如果攻击者能够通过窃取公开信息或通过其他手段计算出 K,则 DH 密钥交换算法的安全性将受到威胁。因此,在实际应用中,通常需要使用其他加密算法来对 DH 密钥交换算法进行补充,以增强其安全性。
总之,DH 密钥交换算法是一种基于离散对数问题的公钥密码学算法,用于在不安全的通信信道上安全地交换密钥。它的安全性基于离散对数难题,通过协商素数、生成私钥、计算公钥、交换公钥和计算共享密钥等步骤来实现。